mFD: General Workflow

About this tutorial

This tutorial describes the basic workflow showing how to compute step by step functional diversity (FD) indices in a multidimensional space using mFD package. Other functions are available and their uses are illustrated in others tutorials.

DATA The dataset used to illustrate this tutorial is a fruits dataset based on 25 types of fruits (i.e. species) distributed in 10 fruits baskets (i.e. assemblages). Each fruit is characterized by five traits values summarized in the following table:

Trait name	Trait measurement	Trait type	Number of classes	Classes code	Unit
Size	Maximal diameter	Ordinal	5	0-1 ; 1-3 ; 3-5 ; 5-10 ; 10-20	cm
Plant	Growth form	Categorical	4	tree; shrub; vine; forb	NA
Climate	Climatic niche	Ordinal	3	temperate ; subtropical ; tropical	NA
Seed	Seed type	Ordinal	3	none ; pip ; pit	NA
Sugar	Sugar	Continuous	NA	NA	g/kg

Overview of the functional framework

The use of the mFD package is based on two datasets:

a data frame summarizing traits values for each species called fruits_traits in this tutorial

# Load data:
data("fruits_traits", package = "mFD")

# Remove fuzzy traits in this tutorial:
fruits_traits <- fruits_traits[ , -c(6:8)]

# Display the table:
knitr::kable(head(fruits_traits),
             caption = "Species x traits data frame")

Species x traits data frame
	Size	Plant	Climate	Seed	Sugar
apple	5-10cm	tree	temperate	pip	103.9
apricot	3-5cm	tree	temperate	pit	92.4
banana	10-20cm	tree	tropical	none	122.3
currant	0-1cm	shrub	temperate	pip	73.7
blackberry	1-3cm	shrub	temperate	pip	48.8
blueberry	0-1cm	forb	temperate	pip	100.0

a matrix summarizing species assemblages called baskets_fruits_weights in this tutorial. Weights in this matrix can be occurrence data, abundance, biomass, coverage, etc. This matrix must have assemblages names in rownames. The studied example works with biomass (i.e. grams of a fruit in a basket) and this matrix looks as follows:

# Load data:
data("baskets_fruits_weights", package = "mFD")

# Display the table:
knitr::kable(as.data.frame(baskets_fruits_weights[1:6, 1:6]), 
      centering = TRUE,
      caption = "Species x assemblages matrix based on the **fruits** dataset")

Species x assemblages matrix based on the **fruits** dataset
	apple	banana
basket_1	400	100
basket_2	200	400
basket_3	200	500
basket_4	300	0
basket_5	200	0
basket_6	100	200

This tutorial will guide you through the main framework, illustrated in the flowchart below, step by step.

Basic framework of the mFD package

1. Know your data

1.1. What types of traits am I using?

The first thing to do before starting analyses is to know your data. To do so, you must be able to characterize the traits you are using (i.e. tell the package what type of traits you are using). That is why mFD package needs a data frame summarizing the type of each trait (i.e. each column of the fruits_traits data frame).

NB You need to set up a data frame with the same columns names as the below example and traits names need to be in the same order as in the fruits_traits data frame:

# Load data:
data("fruits_traits_cat", package = "mFD")

# Remove fuzzy traits in this tutorial:
fruits_traits_cat <- fruits_traits_cat[-c(6:8), ]
# Thus remove the "fuzzy_name" column:
fruits_traits_cat <- fruits_traits_cat[ , -3]

# Display the table:
knitr::kable(head(fruits_traits_cat), 
             caption = "Traits types based on **fruits & baskets** dataset")

Traits types based on **fruits & baskets** dataset
trait_name	trait_type
Size	O
Plant	N
Climate	O
Seed	O
Sugar	Q

The first column contains traits name. The second column contains traits type following this code:

N: nominal trait (factor variable)
O: ordinal traits (ordered variable)
C: circular traits (integer values) (NB circular traits can not be used in mFD function used to compute functional distance but ok for summary function and function to group species into Functional Entities)
Q: quantitative traits (numeric values)
F: fuzzy traits (described with several values defined in several columns in the fruits_traits data frame)

You can add a third column if your dataset use fuzzy traits (then the third column summarizes to which fuzzy trait belongs each column that refers to a fuzzy trait) or if you want to give weight to each traits (then the third column summarizes traits weights).

NOTE The traits types dataframe thus has: two columns if no fuzzy traits and no weight given to traits (columns names: trait_name and trait_type) ; three columns if fuzzy traits (columns names: trait_name,trait_type and fuzzy_name) or if no fuzzy traits and weight given to traits (columns names: trait_name,trait_type and trait_weight). See the first part of the Compute Functional Diversity Hill Indices to see how the fruits_traits and fruits_traits_cat look like with fuzzy traits.

1.2. Summarize my traits

The mFD package helps you to summarize your data using two distinct functions: mFD::sp.tr.summary() and mFD::asb.sp.summary().

The function mFD::sp.tr.summary() summarizes the fruits_traits dataframe and returns a list gathering several tables and lists:

tables with summaries for non-fuzzy & fuzzy traits. For non-fuzzy traits, the table sums up the number of species having each category for ordinal, nominal and circular traits or minimum/first quartile/median/mean/third quartile/maximum for continuous traits. For fuzzy traits, the table sums up minimum/first quartile/median/mean/third quartile/maximum for each category of each fuzzy trait.
a list gathering traits types for non-fuzzy traits
a list gathering modalities of non-continuous and non-fuzzy traits

USAGE

# Species traits summary:
fruits_traits_summ <- mFD::sp.tr.summary(
  tr_cat     = fruits_traits_cat,   
  sp_tr      = fruits_traits, 
  stop_if_NA = TRUE)

## Error in get(paste0(generic, ".", class), envir = get_method_env()) : 
##   object 'type_sum.accel' not found

fruits_traits_summ$"tr_types"                     # Traits types

## $Size
## [1] "ordered" "factor" 
## 
## $Plant
## [1] "factor"
## 
## $Climate
## [1] "ordered" "factor" 
## 
## $Seed
## [1] "ordered" "factor" 
## 
## $Sugar
## [1] "numeric"

fruits_traits_summ$"mod_list"                     # Traits types for non-continuous and non-fuzzy traits

## $Size
## [1] 5-10cm  3-5cm   10-20cm 0-1cm   1-3cm  
## Levels: 0-1cm < 1-3cm < 3-5cm < 5-10cm < 10-20cm
## 
## $Plant
## [1] tree  shrub forb  vine 
## Levels: forb shrub tree vine
## 
## $Climate
## [1] temperate   tropical    subtropical
## Levels: temperate < subtropical < tropical
## 
## $Seed
## [1] pip  pit  none
## Levels: none < pip < pit
## 
## $Sugar
##  [1] 103.9  92.4 122.3  73.7  48.8 100.0 128.2 162.5  73.1  89.9  25.0  16.9
## [13] 152.3 136.6  78.6  91.4 112.0  83.9  97.5  98.5  99.2  44.0  48.9 105.8
## [25]  81.2

1.3. Summarize my assemblages

The second function helping you to summarize your data in the mFD package is mFD::asb.sp.summary(). It summarizes the baskets_fruits_weights matrix and returns a list gathering a matrix, a list and several vectors:

a matrix of species occurrences
a vector gathering species total biomass in all assemblages
a vector gathering the total abundance/biomass per assemblage
a vector gathering species richness per assemblage
a list gathering species names present in each assemblage

USAGE

# Summary of the assemblages * species dataframe:
asb_sp_fruits_summ <- mFD::asb.sp.summary(asb_sp_w = baskets_fruits_weights)

head(asb_sp_fruits_summ$"asb_sp_occ", 3)        # Species occurrences for the first 3 assemblages

##          apple apricot banana currant blackberry blueberry cherry grape
## basket_1     1       0      1       0          0         0      1     0
## basket_2     1       0      1       0          0         0      1     0
## basket_3     1       0      1       0          0         0      1     0
##          grapefruit kiwifruit lemon lime litchi mango melon orange
## basket_1          0         0     1    0      0     0     1      0
## basket_2          0         0     1    0      0     0     1      0
## basket_3          0         0     1    0      0     0     1      0
##          passion_fruit peach pear pineapple plum raspberry strawberry tangerine
## basket_1             1     0    1         0    0         0          1         0
## basket_2             1     0    1         0    0         0          1         0
## basket_3             1     0    1         0    0         0          1         0
##          water_melon
## basket_1           0
## basket_2           0
## basket_3           0

asb_sp_fruits_occ <- asb_sp_fruits_summ$"asb_sp_occ"

asb_sp_fruits_summ$"sp_tot_w"              # Species total biomass in all assemblages

##         apple       apricot        banana       currant    blackberry 
##          1850           200          1400           300           400 
##     blueberry        cherry         grape    grapefruit     kiwifruit 
##           300           950           900           300           400 
##         lemon          lime        litchi         mango         melon 
##          1200           400           300           700          1500 
##        orange passion_fruit         peach          pear     pineapple 
##           900           300           600          1900          1000 
##          plum     raspberry    strawberry     tangerine   water_melon 
##           550           900          1650           300           800

asb_sp_fruits_summ$"asb_tot_w"             # Total biomass per assemblage

##  basket_1  basket_2  basket_3  basket_4  basket_5  basket_6  basket_7  basket_8 
##      2000      2000      2000      2000      2000      2000      2000      2000 
##  basket_9 basket_10 
##      2000      2000

asb_sp_fruits_summ$"asb_sp_richn"           # Species richness per assemblage

##  basket_1  basket_2  basket_3  basket_4  basket_5  basket_6  basket_7  basket_8 
##         8         8         8         8         8         8         8         8 
##  basket_9 basket_10 
##         8         8

asb_sp_fruits_summ$"asb_sp_nm"[[1]]             # Names of species present in the first assemblage

##         apple        banana        cherry         lemon         melon 
##             1             1             1             1             1 
## passion_fruit          pear    strawberry 
##             1             1             1

2. Gathering species into functional entities

If you have many species described by few categorical and ordinal traits only, then you might want to group them into Functional Entities (FE), i.e groups of species with same trait values when species are described with categorical and/or ordinal traits. It is particularly useful when using large datasets with “functionally similar” species.

In this tutorial, this function is not illustrated (FE for the fruits dataset have a single species) and thus functional diversity indices based on FE are not computed. You can have a look to the Compute Functional Diversity Indices based on Functional Entities tutorial for further analysis using FE.

mFD also allows the user to compute FD indices based on Functional Entities (FEs). Computed indices are Functional Redundancy (FRed), Functional OverRedundancy (FORed) and Functional Vulnerability (FVuln) (Mouillot et al. 2014). The fruits & baskets example does not allow to compute FEs, thus FD indices based on FEs can not be compute. Check the Compute functional diversity indices based on Functional Entities tutorial to see how to compute them.

3. Computing distances between species based on functional traits

The next step toward the computation of functional diversity indices is to estimate functional traits-based distances between species in order to build the functional space in which indices will be computed.

To compute trait-based distances, we will use the mFD::funct.dist() function which includes the following arguments:

USAGE

sp_dist_fruits <- mFD::funct.dist(
  sp_tr         = fruits_traits,
  tr_cat        = fruits_traits_cat,
  metric        = "gower",
  scale_euclid  = "scale_center",
  ordinal_var   = "classic",
  weight_type   = "equal",
  stop_if_NA    = TRUE)

sp_tr is the species x trait data frame
tr_cat is the data frame summarizing trait type for each trait
metric is a character string referring to the metric used to compute distances. Two metrics are available and the choice depends on your traits data:
- if all traits are continuous use the Euclidean distance (metric = "euclidean") and check the Compute Functional Diversity Indices based on Only Continuous Traits tutorial which explains how to build a multidimensional space from traits through PCA analysis or considering directly each trait as a dimension.
- if you have non-continuous traits use the Gower distance (metric = "gower") as this method allows traits weighting. This method can also deal with fuzzy traits.
scale_euclid is a character string referring to the way the user wants to scale euclidean traits. You can either chose to scale by range range, use the center transformation center, use the scale transformation scale, use the scale-center transformation scale_center or you can chose not to scale noscale.
ordinal_var is a character string specifying the method to be used for ordinal variables (i.e. ordered). You can either chose to treat ordinal variables as continuous variables (with "classic" option) or to treat ordinal variables as ranks (with metric or podani options, see mFD::funct.dist() help file for details).
weight_type is a character string referring to the type of method to weight traits. You can either chose to define weights using the tr_cat dataframe (cf step 1.1) (user option) or you can chose to give the same weight to all traits (equal option). (NB Using mFD, you can not define weights for fuzzy traits, use gawdis package instead) (NB If you only have continuous traits (see the Continuous traits Framework: using up to the 1.0.6.9 version of the mFD package does not allow weighting, it will be done in a next version of the package. You can use the col.w argument of the PCA function of the FactomineR package.)
stop_if_NA is a logical value to stop or not the process if the sp_tr data frame contains NA. If the sp_tr data frame contains NA you can either chose to compute anyway functional distances (but keep in mind that Functional measures are sensitive to missing traits!) or you can delete species with missing or extrapolate missing traits (see Johnson et al. (2020)).

NB If your data gather a high number of species and/or traits, this function might take time to run (and you might have memory issues).

This function returns a dist object with traits-based distances between all pairs of species:

round(sp_dist_fruits, 3)                 # Output of the function mFD::funct.dist()

##               apple apricot banana currant blackberry blueberry cherry grape
## apricot       0.166                                                         
## banana        0.375   0.541                                                 
## currant       0.391   0.426  0.767                                          
## blackberry    0.376   0.410  0.751   0.084                                  
## blueberry     0.355   0.410  0.731   0.236      0.320                       
## cherry        0.233   0.099  0.558   0.425      0.409     0.389             
## grape         0.380   0.446  0.705   0.372      0.356     0.336  0.347      
## grapefruit    0.192   0.327  0.268   0.501      0.483     0.537  0.426 0.573
## kiwifruit     0.219   0.353  0.595   0.372      0.356     0.364  0.453 0.200
## lemon         0.208   0.343  0.384   0.517      0.433     0.553  0.442 0.589
## lime          0.370   0.404  0.345   0.578      0.494     0.614  0.503 0.650
## litchi        0.466   0.332  0.391   0.658      0.642     0.622  0.233 0.514
## mango         0.395   0.361  0.220   0.786      0.771     0.750  0.362 0.686
## melon         0.285   0.419  0.560   0.407      0.391     0.229  0.518 0.465
## orange        0.117   0.251  0.292   0.474      0.459     0.462  0.351 0.498
## passion_fruit 0.461   0.527  0.414   0.553      0.537     0.516  0.572 0.319
## peach         0.127   0.062  0.503   0.464      0.448     0.472  0.161 0.508
## pear          0.009   0.157  0.384   0.383      0.367     0.353  0.242 0.389
## pineapple     0.557   0.708  0.233   0.734      0.718     0.502  0.791 0.738
## plum          0.156   0.009  0.532   0.435      0.419     0.401  0.090 0.437
## raspberry     0.382   0.416  0.758   0.091      0.007     0.327  0.416 0.363
## strawberry    0.376   0.410  0.751   0.284      0.200     0.120  0.409 0.356
## tangerine     0.153   0.218  0.323   0.444      0.428     0.408  0.281 0.428
## water_melon   0.281   0.415  0.556   0.410      0.395     0.226  0.515 0.462
##               grapefruit kiwifruit lemon  lime litchi mango melon orange
## apricot                                                                 
## banana                                                                  
## currant                                                                 
## blackberry                                                              
## blueberry                                                               
## cherry                                                                  
## grape                                                                   
## grapefruit                                                              
## kiwifruit          0.373                                                
## lemon              0.116     0.389                                      
## lime               0.277     0.550 0.161                                
## litchi             0.459     0.686 0.475 0.336                          
## mango              0.287     0.614 0.403 0.364  0.172                   
## melon              0.308     0.266 0.424 0.585  0.751 0.580             
## orange             0.075     0.302 0.091 0.252  0.384 0.312 0.368       
## passion_fruit      0.453     0.280 0.470 0.331  0.405 0.434 0.546  0.378
## peach              0.265     0.308 0.281 0.442  0.394 0.322 0.357  0.210
## pear               0.184     0.210 0.200 0.361  0.475 0.404 0.276  0.108
## pineapple          0.435     0.562 0.551 0.512  0.624 0.452 0.327  0.460
## plum               0.336     0.363 0.352 0.413  0.323 0.351 0.428  0.261
## raspberry          0.490     0.363 0.426 0.487  0.649 0.777 0.398  0.465
## strawberry         0.483     0.356 0.433 0.494  0.642 0.770 0.191  0.458
## tangerine          0.145     0.372 0.161 0.222  0.314 0.342 0.437  0.070
## water_melon        0.311     0.262 0.427 0.588  0.748 0.576 0.004  0.364
##               passion_fruit peach  pear pineapple  plum raspberry strawberry
## apricot                                                                     
## banana                                                                      
## currant                                                                     
## blackberry                                                                  
## blueberry                                                                   
## cherry                                                                      
## grape                                                                       
## grapefruit                                                                  
## kiwifruit                                                                   
## lemon                                                                       
## lime                                                                        
## litchi                                                                      
## mango                                                                       
## melon                                                                       
## orange                                                                      
## passion_fruit                                                               
## peach                 0.589                                                 
## pear                  0.470 0.119                                           
## pineapple             0.419 0.670 0.551                                     
## plum                  0.518 0.071 0.152     0.701                           
## raspberry             0.543 0.455 0.373     0.725 0.426                     
## strawberry            0.537 0.448 0.367     0.518 0.419     0.207           
## tangerine             0.309 0.280 0.161     0.510 0.209     0.435      0.428
## water_melon           0.542 0.354 0.272     0.324 0.425     0.401      0.194
##               tangerine
## apricot                
## banana                 
## currant                
## blackberry             
## blueberry              
## cherry                 
## grape                  
## grapefruit             
## kiwifruit              
## lemon                  
## lime                   
## litchi                 
## mango                  
## melon                  
## orange                 
## passion_fruit          
## peach                  
## pear                   
## pineapple              
## plum                   
## raspberry              
## strawberry             
## tangerine              
## water_melon       0.434

4. Computing functional spaces & their quality

4.1. Compute multimensional functional spaces and assess their quality

In order to generate a multidimensional space in which functional diversity indices are computed (Mouillot et al. 2013, we will perform a PCoA using the trait-based distances (and if required a functional dendrogram). mFD evaluates the quality of PCoA-based multidimensional spaces according to the deviation between trait-based distances and distances in the functional space (extension of Maire et al. (2015) framework). For that, we will use the mFD::quality.fspaces() function:

USAGE

fspaces_quality_fruits <- mFD::quality.fspaces(
  sp_dist             = sp_dist_fruits,
  maxdim_pcoa         = 10,
  deviation_weighting = "absolute",
  fdist_scaling       = FALSE,
  fdendro             = "average")

## Registered S3 method overwritten by 'dendextend':
##   method     from 
##   rev.hclust vegan

sp_dist is the dist object with pairwise trait-based distance between species as computed in step 3
maxdim_pcoa is the maximum number of PCoA axes to consider to build multidimensional spaces. Actually, the maximum number of dimensions considered depends on the number of PCoA axes with positive eigenvalues.
deviation_weighting refers to the method(s) used to weight the difference between species pairwise distances in the functional space and trait-based distances. You can chose between:
- absolute: absolute differences are used to compute the mean absolute deviation (mad) . It reflects the actual magnitude of errors that will affect FD metrics.
- squared: squared differences are used to compute the root of mean square deviation (rmsd). This weighting puts more weight to the large deviations between trait-based distances and distances in the functional space. misplaced in the functional space.
- Both quality metrics can be used with deviation_weighting = c("absolute", "squared").
fdist_scaling specifies whether distances in the functional space should be scaled before computing differences with trait-based distances. Scaling ensures that trait-based distances and distances in the functional space have the same maximum. Scaling distances implies that the quality of the functional space accounts for congruence in distances rather than their equality.

NOTE The combination of deviation_weighting and fdist_scaling arguments leads to four possible quality metrics: mad, rmsd, mad_scaled and rmsd_scaled

fdendro specifies the clustering algorithm to compute a functional dendrogram. NULL means no dendrogram computed. The chosen algorithm must be one of the method recognized by the stats::hclust() function from the stats package.

This function returns a list various objects:

a data frame gathering for each space (in rows), values of quality metric(s) (in columns)

round(fspaces_quality_fruits$"quality_fspaces", 3)            # Quality metrics of spaces

##                mad
## pcoa_1d      0.150
## pcoa_2d      0.073
## pcoa_3d      0.047
## pcoa_4d      0.040
## pcoa_5d      0.049
## pcoa_6d      0.055
## pcoa_7d      0.060
## pcoa_8d      0.064
## pcoa_9d      0.065
## pcoa_10d     0.065
## tree_average 0.082

lists with details required for other tasks in step 4 to plot functional space quality and in step 5 to plot functional space.

NOTE The space with the best quality has the lowest quality metric. Here, thanks to mad values, we can see that the 4D space is the best one. That is why the following of this tutorial will use this multidimensional space.

4.2. Illustrating the quality of the selected functional spaces

With the mFD package, it is possible to illustrate the quality of PCoA-based multidimensional spaces according to deviation between trait-based distances and distances in the functional space. For that, we use the mFD::quality.fspace.plot() function with the following arguments:

Note: You might encounter the following error while doing plot with mFD: Error in Ops.data.frame(guide_loc, panel_loc) : # ‘==’ only defined for equally-sized data frames} This error is due to a update of the patchwork package, to be able to run the plots, please update the patchwork package to vers. 1.2.0 at least.

USAGE

mFD::quality.fspaces.plot(
  fspaces_quality            = fspaces_quality_fruits,
  quality_metric             = "mad",
  fspaces_plot               = c("tree_average", "pcoa_2d", "pcoa_3d", 
                                 "pcoa_4d", "pcoa_5d", "pcoa_6d"),
  name_file                  = NULL,
  range_dist                 = NULL,
  range_dev                  = NULL,
  range_qdev                 = NULL,
  gradient_deviation         = c(neg = "darkblue", nul = "grey80", pos = "darkred"),
  gradient_deviation_quality = c(low = "yellow", high = "red"),
  x_lab                      = "Trait-based distance")

fspaces_quality is the output of the mFD::quality.fspaces() function (step 4.1).
quality_metric refers to the quality metric used. It should be one of the column name(s) of the table gathering quality metric values (output of mFD::quality.fspaces() called quality_fspaces) (here: fspaces_quality_fruits$quality_fspaces) Thus it can be: mad, rmsd, mad_scaled or rmsd_scaled (see step 4.1)
fspaces_plot refers to the names of spaces for which quality has to be illustrated (up to 10). Names are those used in the output of mFD::quality.fspaces() function showing the values of the quality metric.
name_file refers to the name of file to save (without extension) if the user wants to save the figure. If the user only wants the plot to be displayed, then name_file = NULL.
range_dist, range_dev, range_qdev are arguments to set ranges of panel axes (check function help for further information).
gradient_deviation and gradient_deviation_quality are arguments to set points colors (check function help for further information).
xlab is a parameter to set x-axis label.

This function generates a figure with three panels (in rows) for each selected functional space (in columns). Each column represents a functional space, the value of the quality metric is written on the top of each column. The x-axis of all panels represents trait-based distances. The y-axis is different for each row:

on the first (top) row, the y-axis represents species functional distances in the multidimensional space. Thus, the closer species are to the 1:1 line, the better distances in the functional space fit trait-based ones.
on the second row, the y-axis shows the raw deviation of species distances in the functional space compared to trait-based distances. Thus, the raw deviation reflects the distance to the 1:1 line.
on the third row, the y-axis shows the absolute or squared deviation of the (“scaled”) distance in the functional space. It is the deviation that is taken into account for computing the quality metric.

mFD::quality.fspaces.plot(
  fspaces_quality            = fspaces_quality_fruits,
  quality_metric             = "mad",
  fspaces_plot               = c("tree_average", "pcoa_2d", "pcoa_3d",
                                 "pcoa_4d", "pcoa_5d", "pcoa_6d"),
  name_file                  = NULL,
  range_dist                 = NULL,
  range_dev                  = NULL,
  range_qdev                 = NULL,
  gradient_deviation         = c(neg = "darkblue", nul = "grey80", pos = "darkred"),
  gradient_deviation_quality = c(low = "yellow", high = "red"),
  x_lab                      = "Trait-based distance")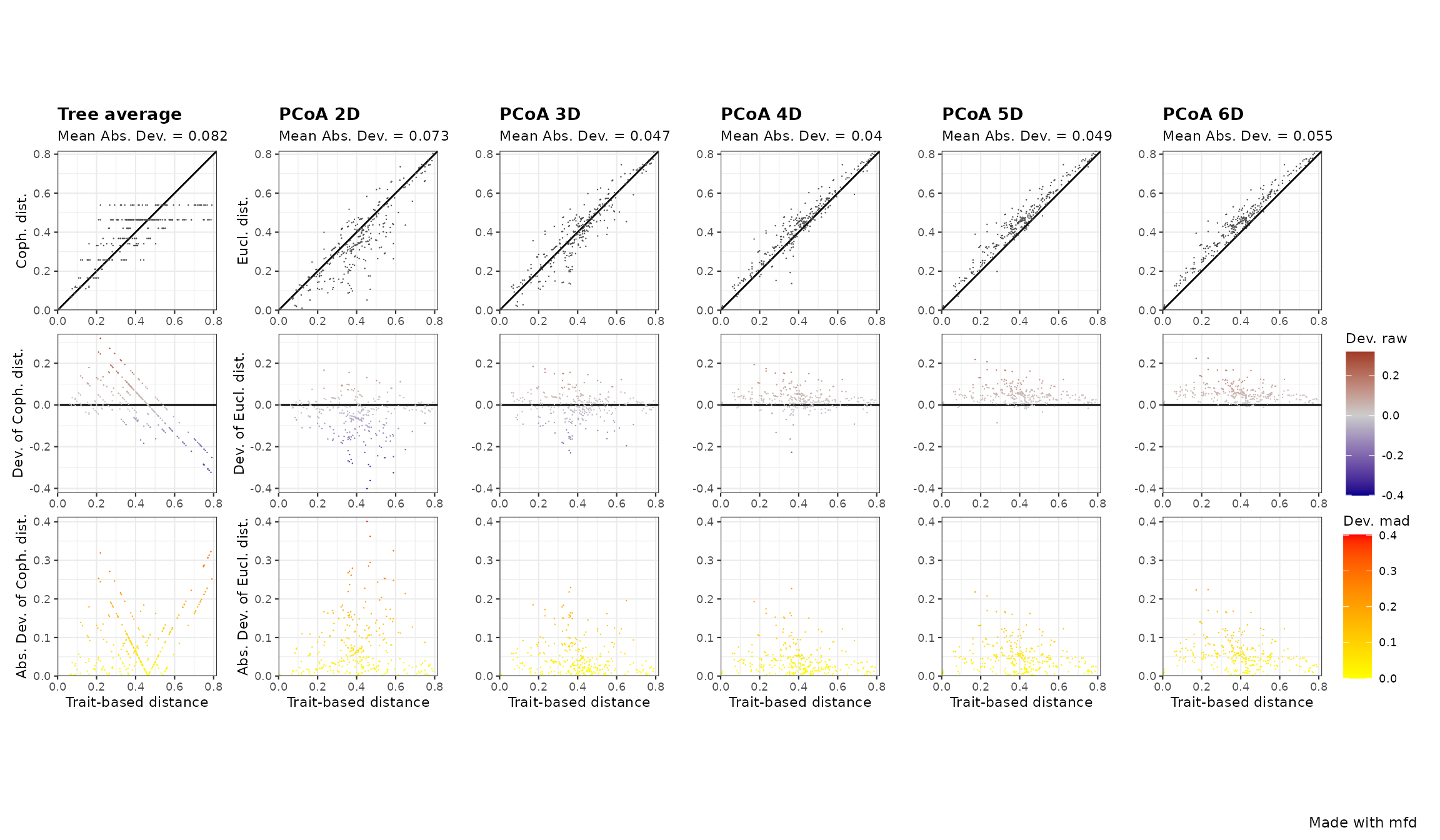

For the 2D space, on the top row there are a lot of points below the 1:1 lines, meaning that distances are overestimated in this multidimensional space. Looking at panels, we can see that the 4D space is the one in which points are the closest to the 1:1 line on the top row,and the closest to the x-axis for the two bottom rows, which reflects a better quality compared to other functional spaces / dendrogram. For the dendrogram, we can see on the top row that species pairs arrange in horizontal lines, meaning that different trait-based distances have then the same cophenetic distance on the dendrogram.

NOTE To know more and better understand how to interpret quality of functional spaces, you should read the Compute and Interpret Quality of Functional Space tutorial.

5. Test correlation between functional axes and traits

mFD allows to test for correlations between traits and functional axes and then illustrate possible correlations. For continuous traits, a linear model is computed and r2 and associated p-value are returned. For non-continuous traits, a Kruskal-Wallis test is computed and eta2 statistic is returned. The function mFD::traits.faxes.cor() allows to test and plot correlation and needs the following arguments:

sp_tr is the species x traits data frame
sp_faxes_coord is a matrix of species coordinates taken from the outputs of the mFD::quality.fspaces() function with columns representing axes on which functional space must be computed. For instance, in this tutorial, we will plot the functional space for 4 and 10 dimensions (cf. the two examples below). The whole sp_faxes_coord can be retrieved through the output of the mFD::quality.fspaces() function:

sp_faxes_coord_fruits <- fspaces_quality_fruits$"details_fspaces"$"sp_pc_coord"

plot is a logical value indicating whether correlations should be illustrated or not. If this option is set to TRUE, traits-axis relationships are plotted through scatterplot for continuous traits and boxplot for non-continuous traits.

mFD::traits.faxes.cor works as follows:

USAGE

fruits_tr_faxes <- mFD::traits.faxes.cor(
  sp_tr          = fruits_traits, 
  sp_faxes_coord = sp_faxes_coord_fruits[ , c("PC1", "PC2", "PC3", "PC4")], 
  plot           = TRUE)

We can print only traits with significant effect on position along one of the axis and look at the plots:

# Print traits with significant effect:
fruits_tr_faxes$"tr_faxes_stat"[which(fruits_tr_faxes$"tr_faxes_stat"$"p.value" < 0.05), ]

##      trait axis           test stat value p.value
## 1     Size  PC1 Kruskal-Wallis eta2 0.308  0.0377
## 3     Size  PC3 Kruskal-Wallis eta2 0.326  0.0325
## 5    Plant  PC1 Kruskal-Wallis eta2 0.471  0.0049
## 6    Plant  PC2 Kruskal-Wallis eta2 0.382  0.0116
## 8    Plant  PC4 Kruskal-Wallis eta2 0.264  0.0360
## 9  Climate  PC1 Kruskal-Wallis eta2 0.731  0.0001
## 13    Seed  PC1 Kruskal-Wallis eta2 0.201  0.0402
## 14    Seed  PC2 Kruskal-Wallis eta2 0.593  0.0005
## 20   Sugar  PC4   Linear Model   r2 0.682  0.0000

# Return plots:
fruits_tr_faxes$"tr_faxes_plot"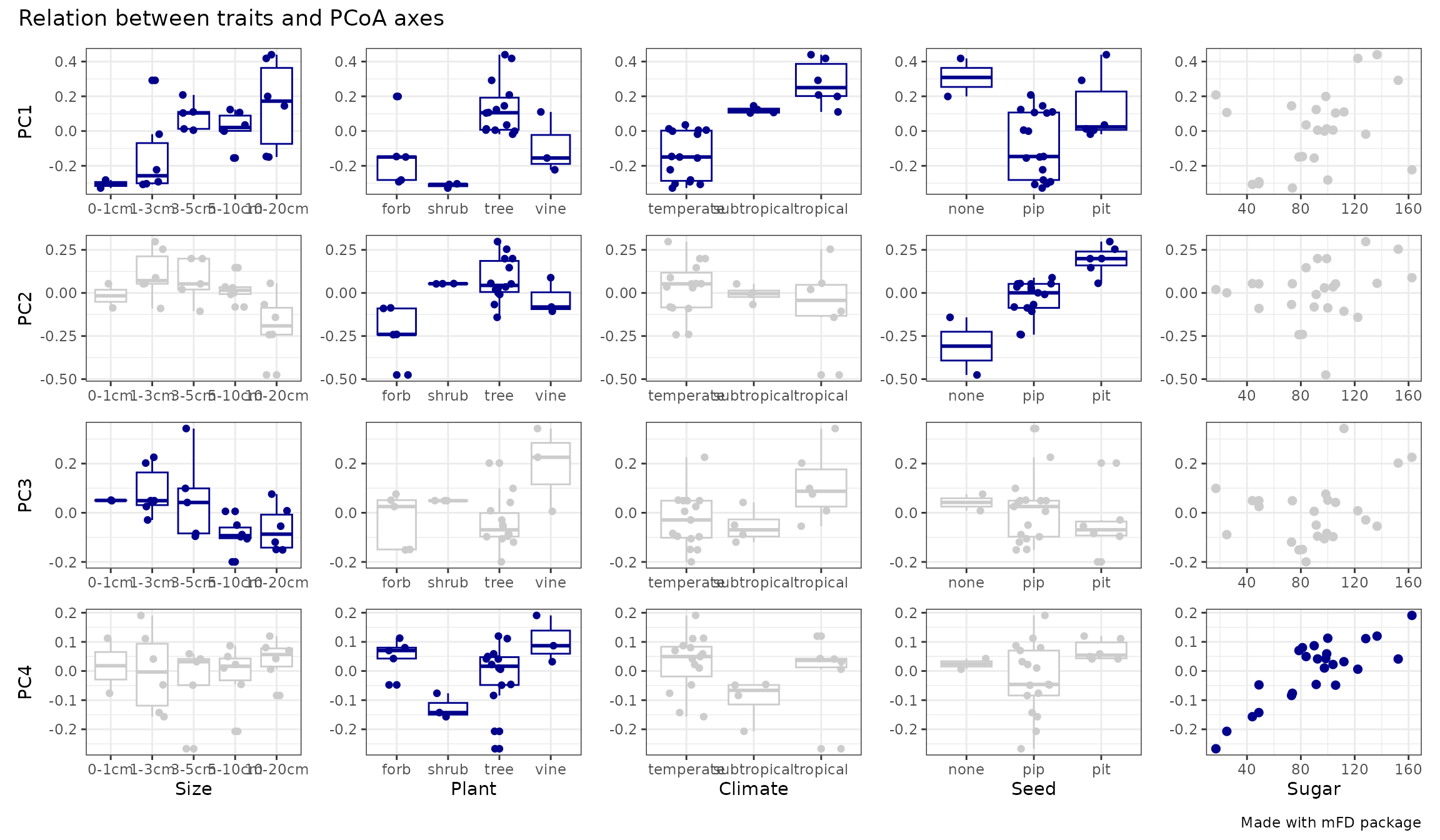

We can thus see that PC1 is mostly driven by Climate (temperate on the left and tropical on the right) and Plant Type (forb & shrub on the left vs tree & vine on the right) and Size (large fruits on the right) with weaker influence of Seed (eta2 < 0.25). Then, PC2 is mostly driven by Seed (no seed on the left and pit seed on the right) with weaker influence of Plant Type. PC3 is driven by only one trait, Size. And finally PC4 is mostly driven by Sugar (high sugar content on the right and low sugar content on the left) with a weaker influence of Plant Type.

6. Plot functional space

Once the user has selected the dimensionality of the functional space, mFD allows you to plot the given multidimensional functional space and the position of species in all 2-dimensions spaces made by pairs of axes.

The mFD::funct.space.plot() function allows to illustrate the position of all species along pairs of space axes.

This function allows to plot with many possibilities to change colors/shapes of each plotted element. Here are listed the main arguments:

sp_faxes_coord is a matrix of species coordinates taken from the outputs of the mFD::quality.fspaces() function with columns representing axes on which functional space must be computed. For instance, in this tutorial, we will plot the functional space for 4 and 10 dimensions (cf. the two examples below). The whole sp_faxes_coord can be retrieved through the output of the mFD::quality.fspaces() function:

sp_faxes_coord_fruits <- fspaces_quality_fruits$"details_fspaces"$"sp_pc_coord"

faxes is a vector containing names of axes to plot. If set to NULL, the first four functional axes will be plotted.
faxes_nm is a vector containing labels of faxes (following faxes vector rank). If NULL, labels follow faxes vector names.
range_faxes is a vector to complete if the user wants to set specific limits for functional axes. If range_faxes = c(NA, NA), the range is computed according to the range of values among all axes.
plot_ch is a logical value used to draw or not the 2D convex-hull filled by the global pool of species. Color, fill and opacity of the convex hull can be chosen through other inputs , please refer to the function’s help.
plot_sp_nm is a vector containing species names to plot. If NULL, no species names plotted. Name size, color and font can be chosen through other inputs, please refer to the function’s help.
plot_vertices is a logical value used to plot or not vertices with a different shape than other species. Be careful: these representations are 2D representations, thus vertices of the convex-hull in the n-multidimensional space can be close to the center of the hull projected in 2D. Color, fill, shape and size of vertices can be chosen through other inputs, please refer to the function’s help.
color_bg is a R color or an hexadecimal color code referring to the color of the background of the plot.
other inputs are used to chose color, fill, size, and shape of species from the global pool, please refer to the function’s help.
check_input is a recurrent argument in the mFD package. It defines whether inputs should be checked before computation or not. Possible error messages will thus be more understandable for the user than R error messages (Recommendation: set it as TRUE).

Here are the plots for the fruits & baskets dataset for the first four PCoA axis:

USAGE

big_plot <- mFD::funct.space.plot(
  sp_faxes_coord  = sp_faxes_coord_fruits[ , c("PC1", "PC2", "PC3", "PC4")],
  faxes           = c("PC1", "PC2", "PC3", "PC4"),
  name_file       = NULL,
  faxes_nm        = NULL,
  range_faxes     = c(NA, NA),
  color_bg        = "grey95",
  color_pool      = "darkgreen",
  fill_pool       = "white",
  shape_pool      = 21,
  size_pool       = 1,
  plot_ch         = TRUE,
  color_ch        = "black",
  fill_ch         = "white",
  alpha_ch        = 0.5,
  plot_vertices   = TRUE,
  color_vert      = "blueviolet",
  fill_vert       = "blueviolet",
  shape_vert      = 23,
  size_vert       = 1,
  plot_sp_nm      = NULL,
  nm_size         = 3,
  nm_color        = "black",
  nm_fontface     = "plain",
  check_input     = TRUE)

Here, the convex-hull of the species pool is plotted in white and axis have the same range to get rid of bias based on different axis scales. Species beign vertices of the 4D convex hull are in purple.

Here are the plots for the fruits & baskets dataset for the first ten PCoA axis:

big_plot <- mFD::funct.space.plot(
  sp_faxes_coord  = sp_faxes_coord_fruits,
  faxes           = NULL,
  name_file       = NULL,
  faxes_nm        = NULL,
  range_faxes     = c(NA, NA),
  color_bg        = "grey95",
  color_pool      = "darkgreen",
  fill_pool       = "white",
  shape_pool      = 21,
  size_pool       = 1,
  plot_ch         = TRUE,
  color_ch        = "black",
  fill_ch         = "white",
  alpha_ch        = 0.5,
  plot_vertices   = TRUE,
  color_vert      = "blueviolet",
  fill_vert       = "blueviolet",
  shape_vert      = 23,
  size_vert       = 1,
  plot_sp_nm      = NULL,
  nm_size         = 3,
  nm_color        = "black",
  nm_fontface     = "plain",
  check_input     = TRUE)

# Plot the graph with all pairs of axes:
big_plot$patchwork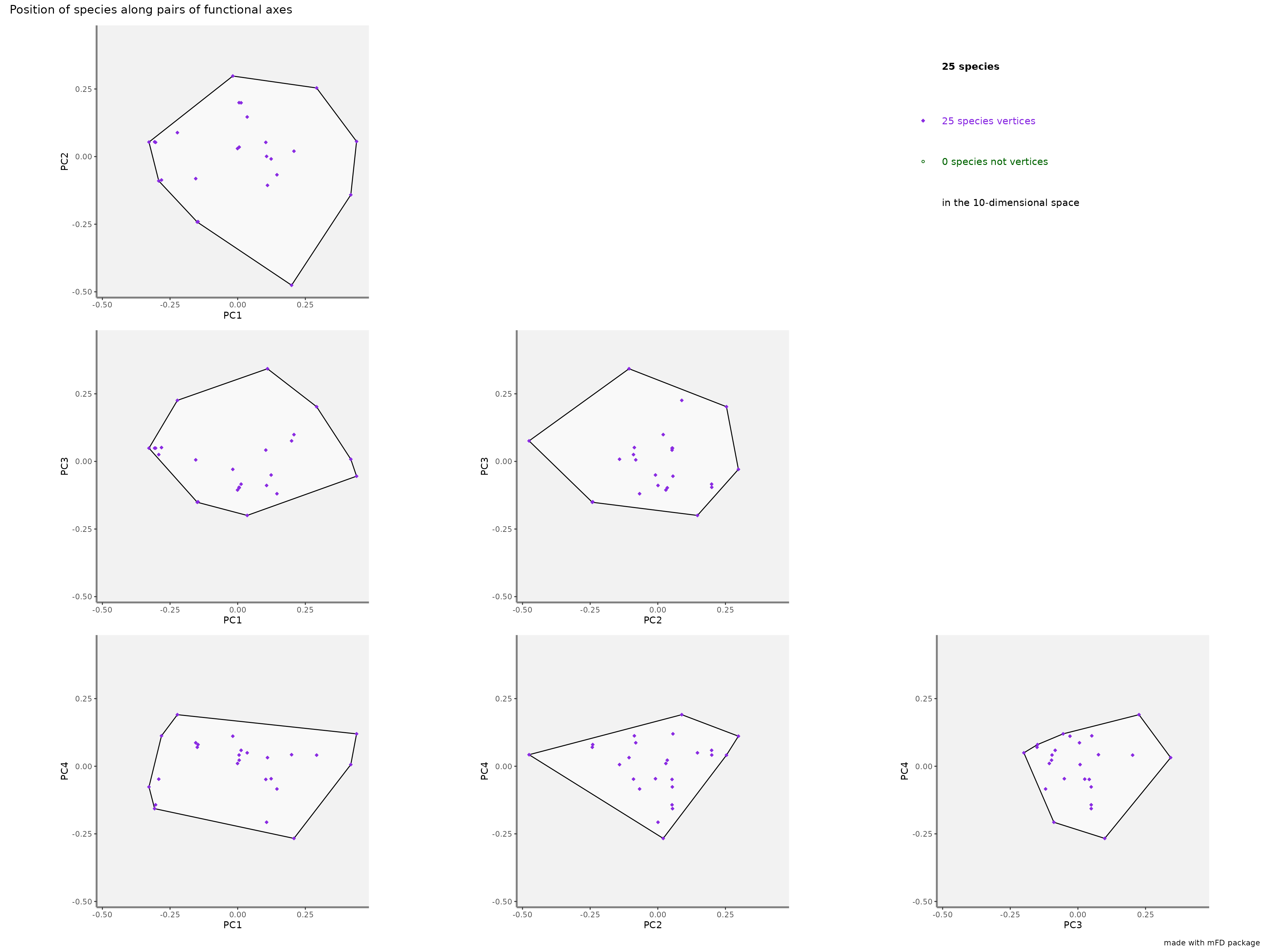

Here, all the species are vertices compared with the last example with only four dimensions.

7. Compute functional diversity indices & plot them

7.1. Functional alpha diversity indices in a multidimensional space

The mFD::alpha.fd.multidim() function allows computing many alpha FD indices:

USAGE

alpha_fd_indices_fruits <- mFD::alpha.fd.multidim(
  sp_faxes_coord   = sp_faxes_coord_fruits[ , c("PC1", "PC2", "PC3", "PC4")],
  asb_sp_w         = baskets_fruits_weights,
  ind_vect         = c("fdis", "fmpd", "fnnd", "feve", "fric", "fdiv", "fori", 
                       "fspe", "fide"),
  scaling          = TRUE,
  check_input      = TRUE,
  details_returned = TRUE)

## basket_1 done 10%

## basket_2 done 20%

## basket_3 done 30%

## basket_4 done 40%

## basket_5 done 50%

## basket_6 done 60%

## basket_7 done 70%

## basket_8 done 80%

## basket_9 done 90%

## basket_10 done 100%

The arguments and their use are listed below:

sp_faxes_coord is the species coordinates matrix. This dataframe gathers only axis of the functional space you have chosen based on step 4.
asb_sp_w is the matrix linking species and assemblages they belong to (summarized in step 1).
ind_vect is a vector with names of diversity functional indices to compute. FD indices computed in the mFD package can be (explanations based on (Mouillot et al. 2013):
- FDis Functional Dispersion: the biomass weighted deviation of species traits values from the center of the functional space filled by the assemblage i.e. the biomass-weighted mean distance to the biomass-weighted mean trait values of the assemblage.
- FRic Functional Richness: the proportion of functional space filled by species of the studied assemblage, i.e. the volume inside the convex-hull shaping species. To compute FRic the number of species must be at least higher than the number of functional axis + 1.
- FDiv Functional Divergence: the proportion of the biomass supported by the species with the most extreme functional traits i.e. the ones located close to the edge of the convex-hull filled by the assemblage.
- FEve Functional Evenness: the regularity of biomass distribution in the functional space using the Minimum Spanning Tree linking all species present in the assemblage.
- FSpe Functional Specialization: the biomass weighted mean distance to the mean position of species from the global pool (present in all assemblages).
- FMPD Functional Mean Pairwise Distance: the mean weighted distance between all species pairs.
- FNND Functional Mean Nearest Neighbour Distance: the weighted distance to the nearest neighbor within the assemblage.
- FIde Functional Identity: the mean traits values for the assemblage. FIde is always computed when FDis is computed.
- FOri Functional Originality: the weighted mean distance to the nearest species from the global species pool.
scaling is a logical value indicating whether indices should be scaled between 0 and 1. If scaling is to be done, this argument must be set to TRUE.
check_input is a recurrent argument in the mFD package. It defines whether inputs should be checked before computation or not. Possible error messages will thus be more understandable for the user than R error messages (Recommendation: set it as TRUE).
details_returned is used if the user wants to store information that are used in graphical functions. If the user wants to plot FD indices, then details_returned must be set to TRUE.

NB Use lowercase letters to enter FD indices names

The function has two main outputs:

a data frame gathering indices values in each assemblage (for FIde values, there are as many columns as there are axes to the studied functional space).

fd_ind_values_fruits <- alpha_fd_indices_fruits$"functional_diversity_indices"
fd_ind_values_fruits

##           sp_richn      fdis      fmpd      fnnd     feve        fric      fdiv
## basket_1         8 0.4763773 0.6255537 0.4050890 0.565326 0.162830681 0.5514453
## basket_2         8 0.7207823 0.7204459 0.6604092 0.754999 0.162830681 0.8064809
## basket_3         8 0.7416008 0.7274367 0.6748312 0.805534 0.162830681 0.8089535
## basket_4         8 0.2958614 0.3426258 0.2258304 0.759802 0.007880372 0.6080409
## basket_5         8 0.3673992 0.3782650 0.2922436 0.843120 0.007880372 0.7288912
## basket_6         8 0.8001980 0.7838356 0.7295674 0.814829 0.147936148 0.8937934
## basket_7         8 0.8121314 0.8092985 0.7566157 0.827061 0.147936148 0.8989094
## basket_8         8 0.4678159 0.5182996 0.3618776 0.566161 0.036480112 0.7113688
## basket_9         8 0.5577452 0.5566262 0.4563761 0.675735 0.036480112 0.7787237
## basket_10        8 0.5505783 0.5501381 0.4118548 0.660085 0.025774304 0.7741681
##                fori      fspe    fide_PC1     fide_PC2    fide_PC3     fide_PC4
## basket_1  0.2024008 0.4127138 -0.01473662 -0.009461738 -0.05670043 -0.001823969
## basket_2  0.2788762 0.5781232  0.01887361 -0.061601373 -0.04427402  0.021249327
## basket_3  0.3067367 0.5888104  0.04724418 -0.056571400 -0.03631846  0.018045257
## basket_4  0.1766279 0.3106937  0.03994897  0.052581211 -0.08413271 -0.001343112
## basket_5  0.2165945 0.3488358  0.02349573  0.039069220 -0.08187248 -0.010262902
## basket_6  0.6071369 0.7930809  0.24320913 -0.114434642  0.01394977  0.025500282
## basket_7  0.4841824 0.7443406  0.13341179 -0.183609095 -0.01782549  0.021494300
## basket_8  0.2538185 0.6363814 -0.24497368  0.036194656  0.04748935 -0.038827673
## basket_9  0.3126927 0.6309078 -0.21021559  0.029339706  0.05516746 -0.041392184
## basket_10 0.1799705 0.4587432 -0.05375867 -0.005743348 -0.05649324  0.041191011

a details list of data frames and sublists gathering information such as coordinates of centroids, distances and identity of the nearest neighbour, distances to the centroid, etc. The user does not have to directly use it but it will be useful if FD indices are then plotted. It can be retrieved through:

details_list_fruits <- alpha_fd_indices_fruits$"details"

Then, you can plot functional indices using the mFD::alpha.multidim.plot() function as follows:

USAGE

plots_alpha <- mFD::alpha.multidim.plot(
  output_alpha_fd_multidim = alpha_fd_indices_fruits,
  plot_asb_nm              = c("basket_1", "basket_5"),
  ind_nm                   = c("fdis", "fide", "fnnd", "feve", "fric", 
                               "fdiv", "fori", "fspe"),
  faxes                    = NULL,
  faxes_nm                 = NULL,
  range_faxes              = c(NA, NA),
  color_bg                 = "grey95",
  shape_sp                 = c(pool = 3, asb1 = 21, asb2 = 21),
  size_sp                  = c(pool = 0.7, asb1 = 1, asb2 = 1),
  color_sp                 = c(pool = "grey50", asb1 = "#1F968BFF", asb2 = "#DCE319FF"),
  color_vert               = c(pool = "grey50", asb1 = "#1F968BFF", asb2 = "#DCE319FF"),
  fill_sp                  = c(pool = NA, asb1 = "#1F968BFF", asb2 = "#DCE319FF"),
  fill_vert                = c(pool = NA, asb1 = "#1F968BFF", asb2 = "#DCE319FF"),
  color_ch                 = c(pool = NA, asb1 = "#1F968BFF", asb2 = "#DCE319FF"),
  fill_ch                  = c(pool = "white", asb1 = "#1F968BFF", asb2 = "#DCE319FF"),
  alpha_ch                 = c(pool = 1, asb1 = 0.3, asb2 = 0.3),
  shape_centroid_fdis      = c(asb1 = 22,  asb2 = 24),
  shape_centroid_fdiv      = c(asb1 = 22,  asb2 = 24),
  shape_centroid_fspe      = 23,
  color_centroid_fspe      = "black",
  size_sp_nm               = 3, 
  color_sp_nm              = "black",
  plot_sp_nm               = NULL,
  fontface_sp_nm           = "plain",
  save_file                = FALSE,
  check_input              = TRUE)

As you can see, this function has a lot of arguments: most of them are graphical arguments allowing the user to chose colors, shapes, sizes, scales, etc. This tutorial only presents main arguments. To learn about the use of graphical arguments, check the function help file. The main arguments of this function are listed below:

output_alpha_fd_multidim is the output of the `mFD::alpha.fd.multidim() function.
plot_asb_nm is a vector gathering name(s) of assemblage(s) to plot.
ind_vect is a vector gathering FD indices to plot. Plots are available for FDis, FIde, FEve, FRic, FDiv, FOri, FSpe, and FNND.
faxes is a vector containing names of axes to plot. You can only plot from two to four axes labels for graphical reasons.
faxes_nm is a vector with axes labels if the user ants different axes labels than faxes ones.
range_faxes is a vector with minimum and maximum values for axes. If range_faxes = c(NA, NA), the range is computed according to the range of values among all axes, all axes having thus the same range. To have a fair representation of species positions in all plots, all axes must have the same range.
plot_sp_nm is a vector containing species names to plot. If NULL, then no name is plotted.
size, color, fill, and shape arguments for each component of the graphs i.e. species of the global pool, species of the studied assemblage(s), vertices, centroids and segments. If you have to plot two assemblages, then inputs should be formatted as follow: c(pool = ..., asb1 = ..., asb2 = ...) for inputs used for global pool and studied assemblages and c(asb1 = ..., asb2 = ...) for inputs used for studied assemblages only.
check_input is a recurrent argument in mFD. It defines whether inputs should be checked before computation or not. Possible error messages will thus be more understandable for the user than R error messages (Recommendation: set it as TRUE.

Then, using these arguments, here are the output plots for the fruits & baskets dataset:

FRic representation: the colored shapes reflect the convex-hull of the studied assemblages and the white shape reflects the convex-hull of the global pool of species:

plots_alpha$"fric"$"patchwork"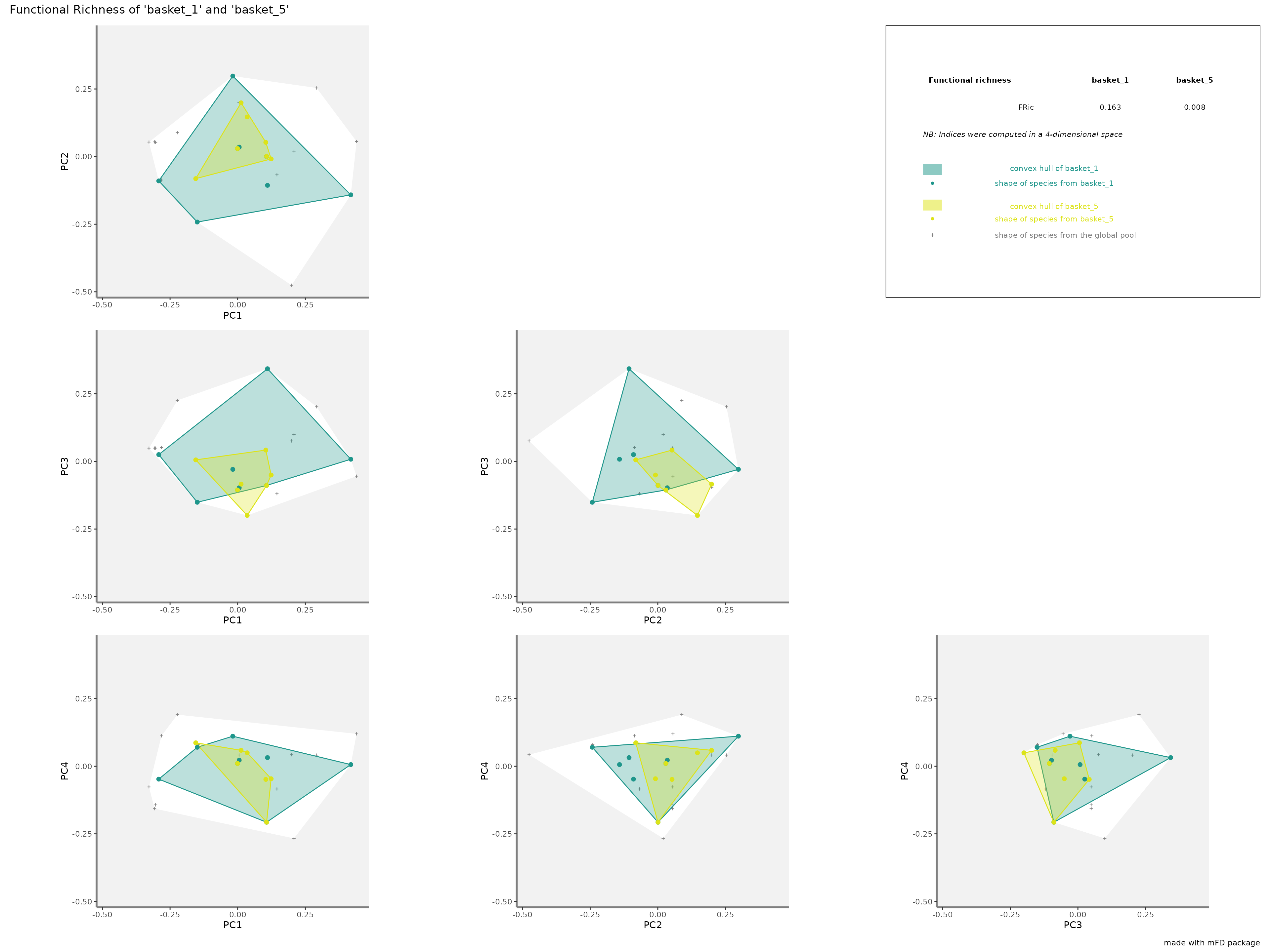

FDiv representation: the gravity centers of vertices (i.e. species with the most extreme functional traits) of each assemblages are plotted as a square and a triangle. Species of each assemblage have different size given their relative weight into the assemblage.

plots_alpha$"fdiv"$"patchwork"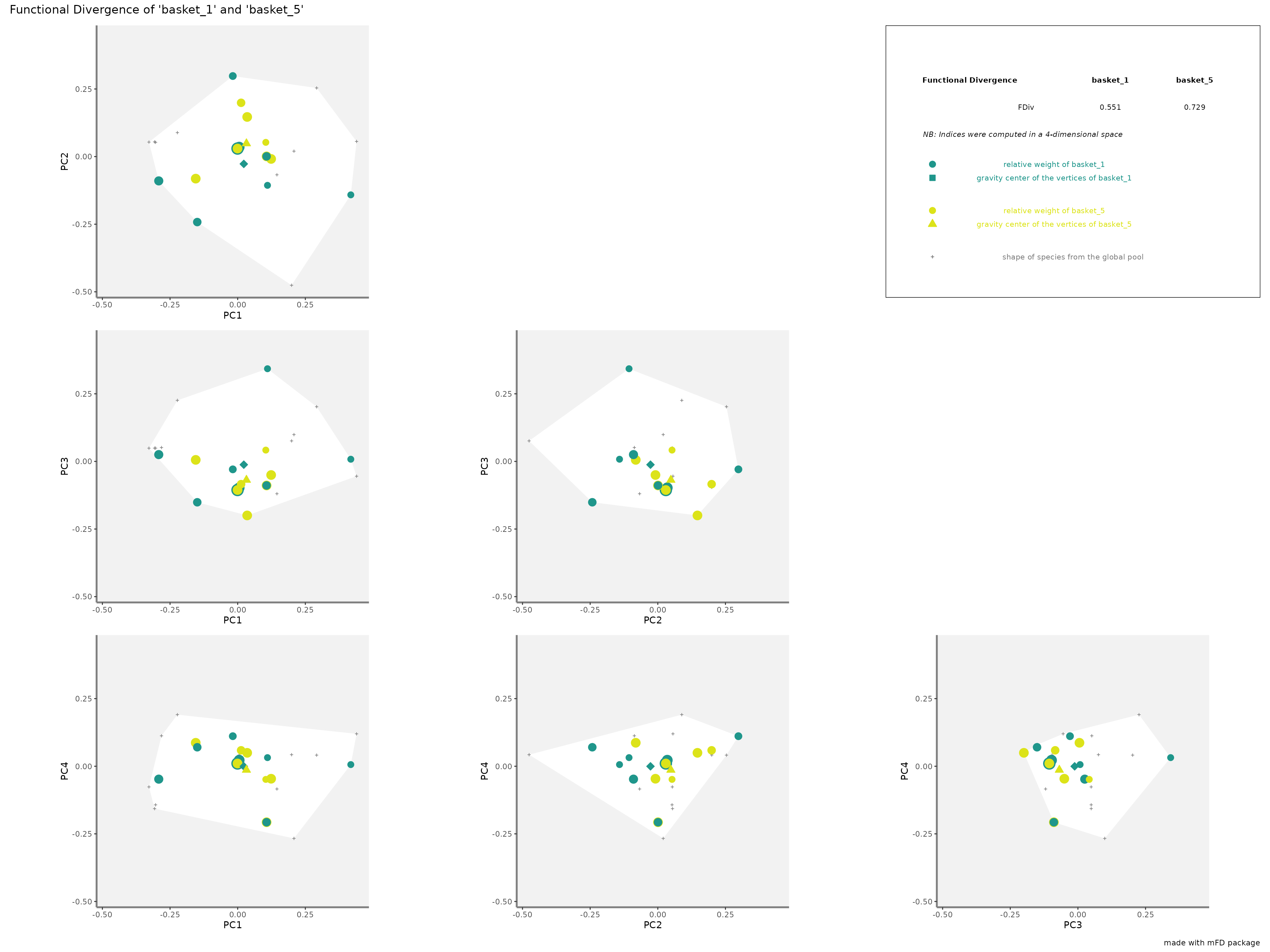

FSpe representation: colored traits represent distances of each species from a given assemblage to the center of gravity of the global pool (i.e center of the functional space). the center of gravity is plotted with a purple diamond. Species of each assemblage have different size given their relative weight into the assemblage.

plots_alpha$"fspe"$"patchwork"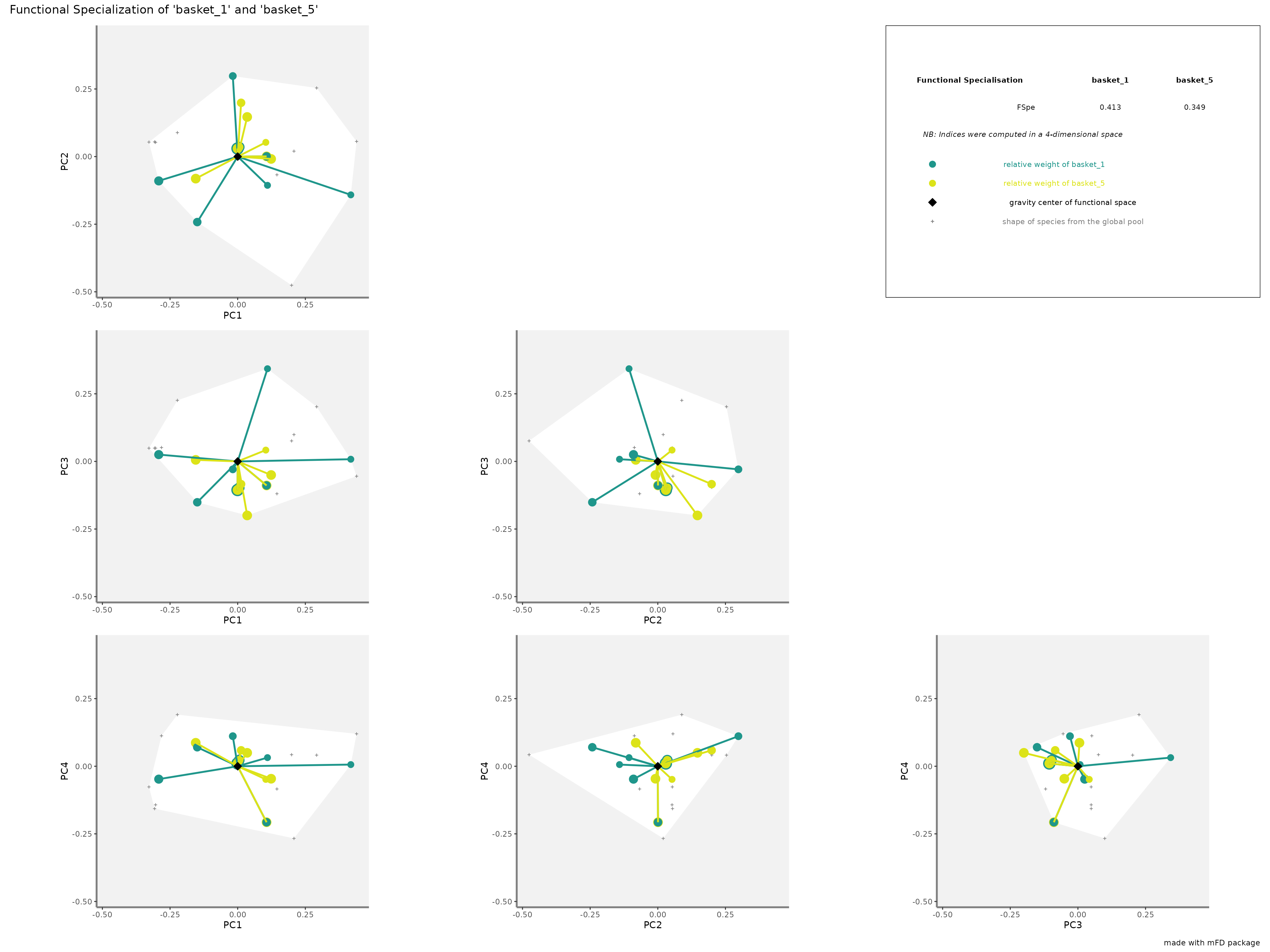

FDis representation: colored traits represent distances of each species from a given assemblage to the center of gravity of species of the assemblage (defined by FIde values). The center of gravity of each assemblage is plotted using a square and a triangle. Species of each assemblage havedifferent size given their relative weight into the assemblage.

plots_alpha$"fdis"$"patchwork"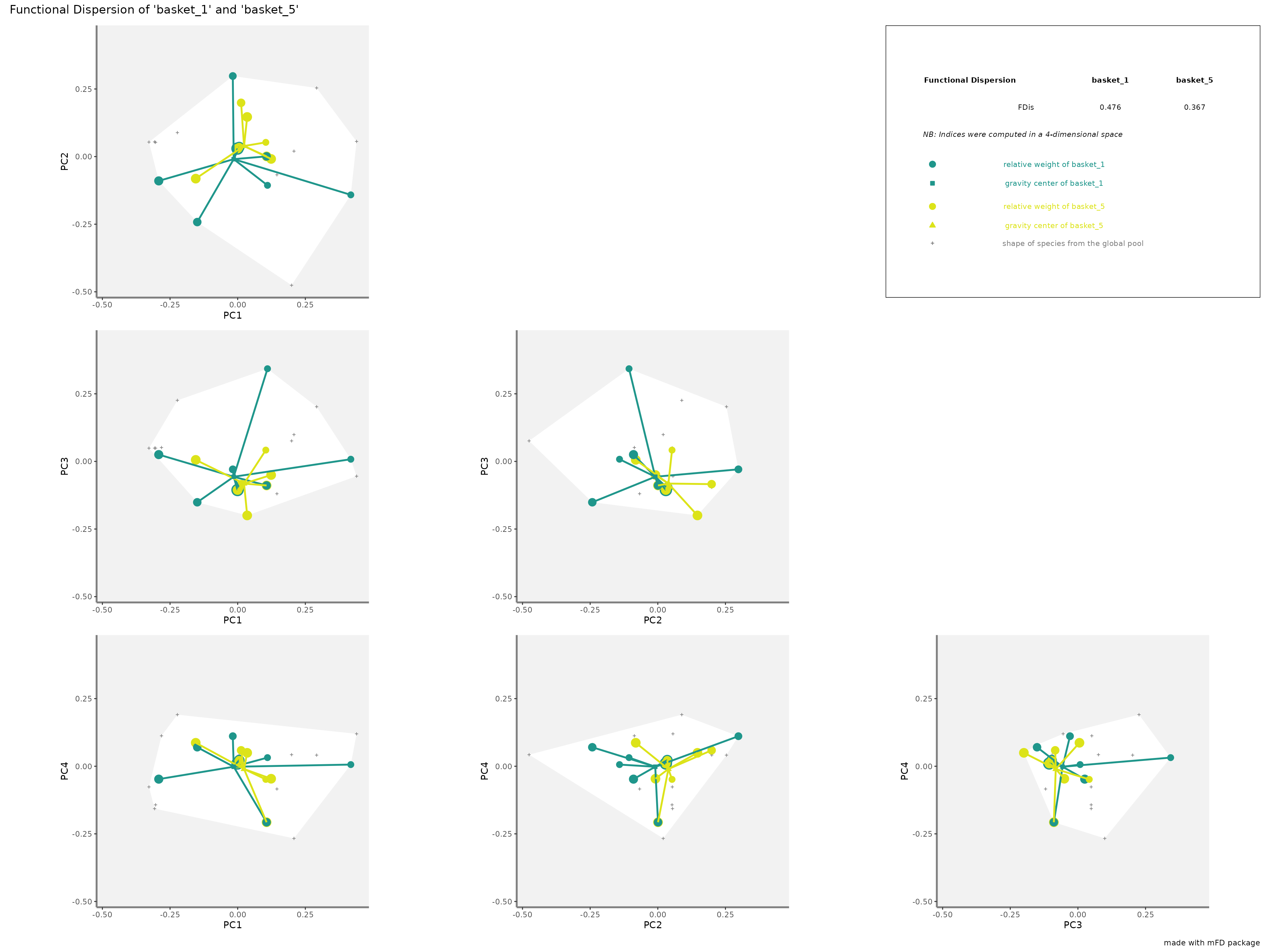

FIde representation:colored lines refer to the weighted average position of species of each assemblage along each axis. Species of each assemblage have different size given their relative weight into the assemblage.

plots_alpha$"fide"$"patchwork"

FEve representation: colored traits represent the Minimum Spanning Tree linking species of each assemblage. Species of each assemblage have different size given their relative weight into the assemblage.

plots_alpha$"feve"$"patchwork"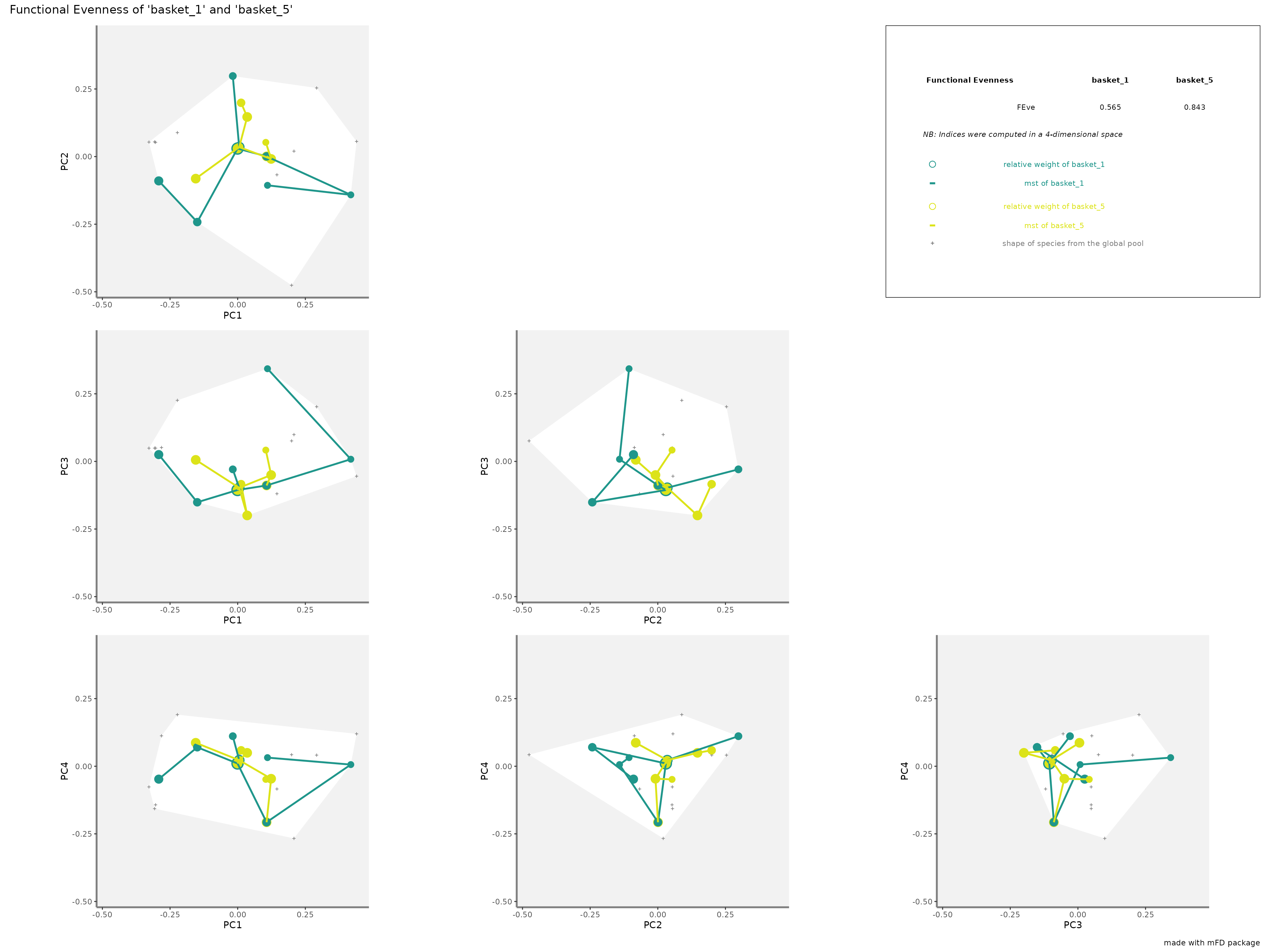

FOri representation: colored arrows represent the distances of each species from each assemblage to the nearest species in the global species pool. Species of each assemblage have different size given their relative weight into the assemblage.

plots_alpha$"fori"$"patchwork"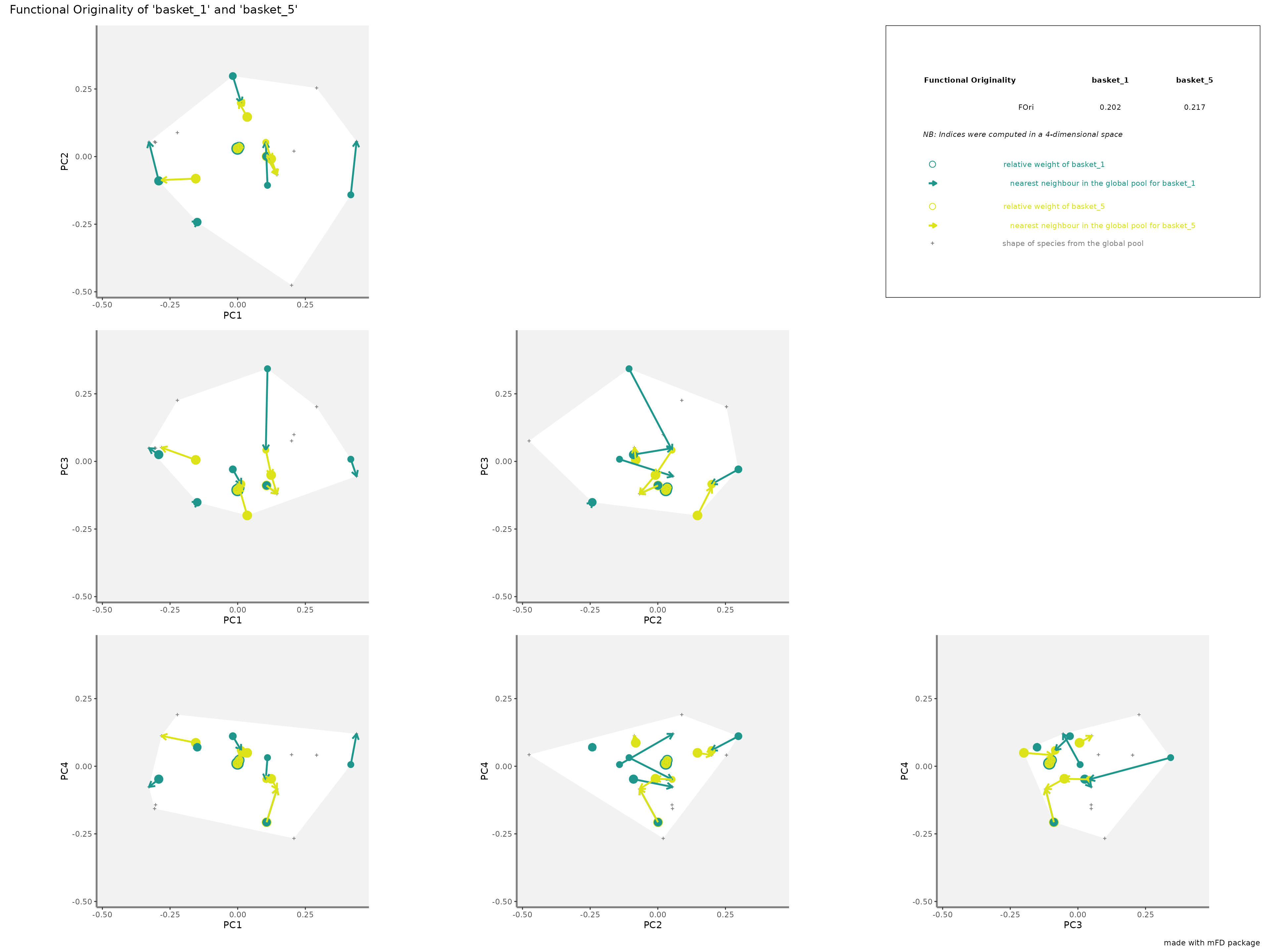

FNND representation: colored arrows represent the distances of each species from each assemblage to the nearest species in the studied assemblage. Species of each assemblage have different size given their relative weight into the assemblage.

plots_alpha$"fnnd"$"patchwork"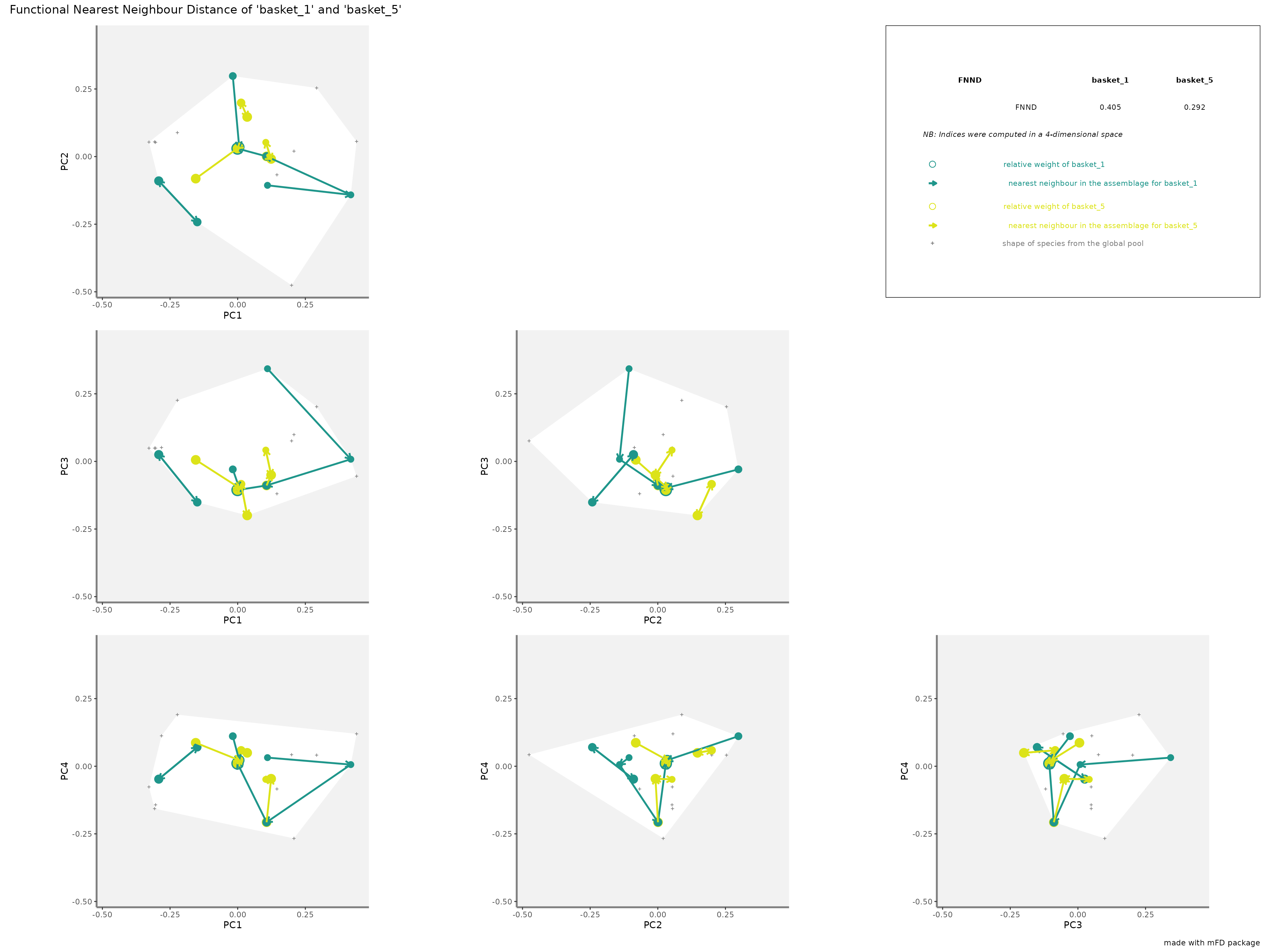

7.2. Functional beta diversity indices based on multidimensional space

NOTE: Some Mac OS X 10.15 may encounter some issues with the beta_*() functions.

mFD package allows you to compute beta diversity indices for each assemblage pairs following Villeger et al. 2013. For that we will use the mFD::beta.fd.multidim() function.

NOTE This function can compute two families of functional beta diversity indices, either Jaccard or Sorensen.

In this example, we will use Jaccard index. For each assemblages pair, the dissimilarity index is decomposed into two additive components: turnover and nestedness-resultant. NB The turnover component is the highest if there is no shared traits combination between the two assemblages. The nestedness component is the highest if one assemblage hosts a small subset of the functional strategies present in the other.

The mFD::beta.fd.multidim() function has the main following arguments:

USAGE

beta_fd_indices_fruits <- mFD::beta.fd.multidim(
      sp_faxes_coord   = sp_faxes_coord_fruits[ , c("PC1", "PC2", "PC3", "PC4")],
      asb_sp_occ       = asb_sp_fruits_occ,
      check_input      = TRUE,
      beta_family      = c("Jaccard"),
      details_returned = TRUE)

sp_faxes_coord is the species coordinates matrix. This dataframe gathers only axis of the functional space you have chosen based on step 4.
asb_sp_occ is the matrix of occurrence (coded as 0/1) of species assemblages (summarized in step 1).
check_input is a recurrent argument in the mFD package. It defines whether inputs should be checked before computation or not. Possible error messages will thus be more understandable for the user than R error messages (Recommendation: set it as TRUE.
beta_family a character string for the type of beta-diversity index to compute, it can either be Jaccard or Sorensen.
details_returned is a logical value indicating whether details of outputs must be stored. It should be stored if you plan to use the graphical function to illustrate beta diversity indices thereafter.
There are also other arguments for parallelisation options. Check the function help file for more explanation.

The function returns a list containing:

a dist object with beta indices values for each pair of assemblages

a list containing details such as inputs, vertices of the global pool and of each assemblage and FRic values for each assemblage

a vector containing the FRic value for each assemblage retrieved through the details_beta list
a list of vectors containing names of species being vertices of the convex hull for each assemblage retrieved through the details_beta list

Then, the package allows the user to illustrate functional beta-diversity indices for a pair of assemblages in a multidimensional space using the mFD::beta.multidim.plot() function. The output of this function is a figure showing the overlap between convex hulls shaping each of the two species assemblages.

The plotting function has a large number of arguments, allowing the user to chose graphical options. Arguments are listed below:

USAGE

beta_plot_fruits <- mFD::beta.multidim.plot(
  output_beta_fd_multidim = beta_fd_indices_fruits,
  plot_asb_nm             = c("basket_1", "basket_4"),
  beta_family             = c("Jaccard"),
  plot_sp_nm              = c("apple", "lemon", "pear"),
  faxes                   = paste0("PC", 1:4),
  name_file               = NULL,
  faxes_nm                = NULL,
  range_faxes             = c(NA, NA),
  color_bg                = "grey95",
  shape_sp                = c("pool" = 3.0, asb1 = 22, asb2 = 21),
  size_sp                 = c("pool" = 0.8, asb1 =  1, asb2 =  1),
  color_sp                = c("pool" = "grey50", asb1 = "blue", asb2 = "red"),
  fill_sp                 = c("pool" = NA, asb1 = "white", asb2 = "white"),
  fill_vert               = c("pool" = NA, asb1 = "blue", asb2 = "red"),
  color_ch                = c("pool" = NA, asb1 = "blue", asb2 = "red"),
  fill_ch                 = c("pool" = "white", asb1 = "blue", asb2 = "red"),
  alpha_ch                = c("pool" = 1, asb1 = 0.3, asb2 = 0.3),
  nm_size                 = 3,
  nm_color                = "black",
  nm_fontface             = "plain",
  check_input             = TRUE)

output_beta_fd_multidim is the output of the mFD::beta.fd.multidim() function retrieved before as beta_fd_indices.
plot_asb_nm is a vector containing the name of the two assemblages to plot. Here plots of indices will be shown for basket_1 and basket_4.
beta_family refers to the family of the plotted index. It must be the same as the family chosen to compute beta functional indices values with the mFD::beta.fd.multidim() function.
plot_sp_nm is a vector containing the names of species the user want to plot, if any. If no the user does not want to plot any species name, then this argument must be set up to NULL. Here, apple, cherry and lemon will be plotted on the graph.
faxes is a vector containing the names of the functional axes of the plotted functional space. Here, the figure will be plotted for PC1, PC2 and PC3. This function allows you to plot between two and four axes for graphical reasons.
name_file is a character string with the name of the file to save the figure (without extension). If the user does not want to save the file and only display it, this argument must be set up to NULL.
faxes_nm is a vector containing the axes labels for the figure if the user wants to set up different labels than those contained in faxes.
range_faxes is a vector with minimum and maximum values of functional axes. To have a fair representation of the position of species in all plots, axes should have the same range. If the user wants the range to be computed according to the range of values among all axes, this argument must be set up to c(NA, NA).
check_input is a recurrent argument in the mFD package. It defines whether inputs should be checked before computation or not. Possible error messages will thus be more understandable for the user than R error messages (Recommendation: set it as TRUE)
Others arguments to set up colors, shapes, sizes and, text fonts are also available. For more information about them, read the function help file.

Then, the function returns each graph for each functional axes combination and also a multipanel plot with all combinations of axes and the graph caption.

For each assemblage, the associated convex hull is plotted in a different colour and indices values are printed on the right corner of the plot. Vertices of the convex hull of a given assemblage can be plotted with a different symbol such as in this example. Species of all assemblages are plotted with gray cross and the associated convex hull is plotted in white.

References

Johnson et al. (2020) Handling missing values in trait data. Global Ecology and Biogeography, 30, 51-62.
Maire et al. (2015) How many dimensions are needed to accurately assess functional diversity? A pragmatic approach for assessing the quality of functional spaces. Global Ecology and Biogeography, 24, 728-740.
Mouillot et al. (2013) A functional approach reveals community responses to disturbances. Trends in Ecology and Evolution, 28, 167-177.
Mouillot et al. (2014) Functional over-redundancy and high functional vulnerability in global fish faunas on tropical reefs. PNAS, 38, 13757-13762.

Camille Magneville

2024-12-19

About this tutorial

Overview of the functional framework

1. Know your data

1.1. What types of traits am I using?

1.2. Summarize my traits

1.3. Summarize my assemblages

2. Gathering species into functional entities

3. Computing distances between species based on functional traits

4. Computing functional spaces & their quality

4.1. Compute multimensional functional spaces and assess their quality

4.2. Illustrating the quality of the selected functional spaces

5. Test correlation between functional axes and traits

6. Plot functional space

7. Compute functional diversity indices & plot them

7.1. Functional alpha diversity indices in a multidimensional space

7.2. Functional beta diversity indices based on multidimensional space

References